1. Множество и его элементы 

Множество – это набор определённых объектов, которые имеют общее свойство. Например, множество книг, множество карандашей, множество машин, множество студентов университета, множество чётных чисел. Множества обозначают прописными буквами латинского алфавита: A, B, C, D и так далее. 

Объекты, которые составляют данное множество, – это элементы множества. Элементы множества обозначают строчными буквами латинского алфавита: a, b, c, d и так далее. 

Если элемент a принадлежит множеству A, то пишут a ∈ A (а принадлежит множеству а). Если элемент b не принадлежит множеству A, то пишут b ∉ A (бэ не принадлежит множеству а). 

Множество можно задать с помощью перечисления его элементов. Например, если М – это множество положительных делителей числа 12, то М = {1, 2, 3, 4, 6, 12}. Множество простых делителей числа 12 имеет вид: M₁ = {2, 3}. 

 

2. Операции над множествами 

Если все элементы множества В – это также элементы множества А, то говорят, что множество В – это подмножество множества A, то есть B ⊂ A. 

Пример. Рассмотрим множества положительных и простых делителей числа 12: М = {1, 2, 3, 4, 6, 12} и M₁ = {2, 3}. Все элементы множества M₁ – это элементы множества M. Поэтому M₁ – это подмножество M: M₁ ⊂ M. 

Если множество не содержит элементов, то это пустое множество ∅. Пустое множество – это подмножество любого множества. 

Каждое множество – это подмножество самого себя. 

Для каждого множества можно назвать его подмножества. 

Пример. Выпишем все подмножества множества A = {x, y, z}. 

Имеем: ∅, {x}, {y}, {z}, {x, y}, {x, z}, {y, z}, {x, y, z}. 

Над множествами можно выполнять операции. 

Объединение множеств А и В (А ∪ В) – это множество, содержащее все элементы, которые принадлежат хотя бы одному из данных множеств: или множеству А, или множеству В. 

Пересечение множеств А и В (А ∩ В) – это множество, содержащее все элементы, которые принадлежат и множеству А, и множеству В. 

Пример. Найдём объединение и пересечение множеств A = {1, 2, 3, 4, 5, 6} и B = {2, 4, 6, 8, 10}. 

Имеем: А ∪ В = {1, 2, 3, 4, 5, 6, 8, 10}, А ∩ В = {2, 4, 6}. 

 

3. Числовые множества 

1, 2, 3, 4, … – это натуральные числа. Все натуральные числа можно записать как множество N. 

N = {1; 2; 3; …}– это множество натуральных чисел. 

Натуральные числа 1, 2, 3, 4, … – это элементы множества N. 

19 – это натуральное число или 19 – это элемент N. Это выражение можно записать так: 19 ∈ N (девятнадцать принадлежит множеству эн). 

0 – это ненатуральное число или 0 – это не элемент N. Это выражение можно записать так: 0 ∉ N (нуль не принадлежит множеству эн). 

Отрицательные числа – это ненатуральные числа. Отрицательные числа не принадлежат множеству N. 

Пример. 135 ∈ N, 6 ∈ N, 0 ∉ N, –8 ∉ N, –271 ∉ N. 

… –4, –3, –2, –1, 0, 1, 2, 3, 4, … – это целые числа. 

Все целые числа можно записать как множество Z. 

Z = {… –4, –3, –2, –1, 0, 1, 2, 3, 4, … } – это множество целых чисел. 

Натуральные числа и нуль – это целые числа, они принадлежат множеству Z. Дроби – это нецелые числа, они не принадлежат множеству Z. 

Пример. 23 ∈ Z, 0 ∈ Z, –8 ∈ Z, –271 ∈ Z,  ∉ Z, 0,1 ∉ Z, 0,333333… ∉ Z. 

Число, которое можно записать в виде  (где p – целое число, а q – натуральное число) – это рациональное число. Например, числа 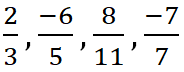– это рациональные числа. 

Все рациональные числа можно записать как множество рациональных чисел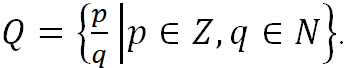  

Целые числа 5, –1, 81 – это тоже рациональные числа, потому что их можно записать как дроби со знаменателем 1: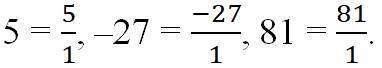  

Конечные и бесконечные периодические десятичные дроби – это тоже рациональные числа. Конечная десятичная дробь 0,06 – это рациональное число, потому что 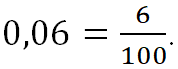Бесконечная периодическая десятичная дробь 0,444444… = 0,(4) – это тоже рациональное число, потому что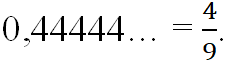  

Бесконечные непериодические десятичные дроби – это нерациональные числа. 

Пример.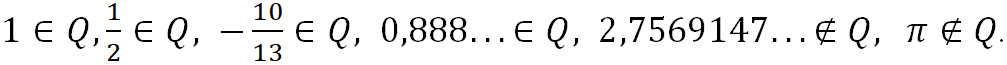  

Число, которое можно записать в виде бесконечной непериодической десятичной дроби, – это иррациональное число. Все иррациональные числа можно записать как множество J – множество иррациональных чисел. 

Все рациональные числа не принадлежат множеству J. 

Пример.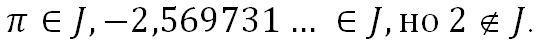  

Все рациональные и иррациональные числа – это действительные числа. Все действительные числа можно записать как множество R – множество действительных чисел. Множество R – это объединение множеств Q и J, множество Q – это подмножество множества R, множество J – это подмножество множества R. 

 

Целые числа – это рациональные числа. В этом случае говорят, что множество Z – это подмножество множества Q, то есть  

Натуральные числа – это целые числа, поэтому множество N – это подмножество множества Z, то есть