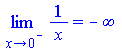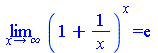Вычисление суммы ряда, произведения и предела
Вычисление суммы членов некоторой последовательности f (k) при изменении целочисленного индекса k от значения m до значения n, т.е. 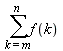 , является достаточно распространенной операцией математического анализа.
, является достаточно распространенной операцией математического анализа.
Для вычисляемой и инертной форм вычисления сумм служат функции sum и Sum. Отметим, что многие функции Maple имеют вычисляемую и инертную формы.
Вычисляемая форма суммы.
Инертная форма суммы.
Оформление результатов расчета с использованием инертной и вычисляемой форм.
| > |
Sum(k^2,k=1..10)=sum(k^2,k=1..10); |
Отметим, что если переменной − индексу k к моменту вычисления суммы уже присвоено какое-либо значение, то функция sum приведет к ошибке.
| > |
k:=125;
sum(k^2,k = 1 .. 10); |
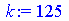 |
| Error, (in sum) summation variable previously assigned, second argument evaluates to 125 = 1 .. 10 |
Для того чтобы избежать ошибки, следует использовать одинарные кавычки, как показано ниже.
Функция value служит для вычисления инертных форм.
| > |
restart:
S:=Sum('k^2','k'=1..10);
value(S); |
Многие бесконечные суммы сходятся к определенным значениям и Maple способен их вычислить.
| > |
Sum(1/k!, k=0..infinity)=sum(1/k!, k=0..infinity); |
| > |
Sum(1/k^2, k=1..infinity)=sum(1/k^2, k=1..infinity); |
Для вычисления произведений служат функции product и Product.
| > |
Product(k^2,k =1..5)=product(k^2,k = 1..5); |
Для вычисления пределов служат функции limit и Limit. Вычислим предел функции  в точке
в точке 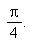
| > |
Limit(12*sin(x),x=Pi/4)=limit(12*sin(x),x=Pi/4); |
Предел функции 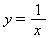 в точке x = 0.
в точке x = 0.
| > |
Limit(1/x,x=0)=limit(1/x,x=0); |
Предел справа от нуля.
| > |
Limit(1/x,x=0,right)=limit(1/x,x=0,right); |
Предел слева от нуля.
| > |
Limit(1/x,x=0,left)=limit(1/x,x=0,left); |
Первый замечательный предел.
| > |
Limit(sin(x)/x,x=0)=limit(sin(x)/x,x=0); |
Второй замечательный предел.
| > |
Limit((1+1/x)^x,x=infinity)=limit((1+1/x)^x,x=infinity); |
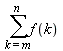 , является достаточно распространенной операцией математического анализа.
, является достаточно распространенной операцией математического анализа. 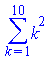
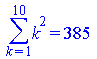
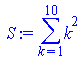
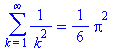
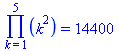
![]() в точке
в точке ![]()
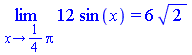
![]() в точке x = 0.
в точке x = 0.