Поиск экстремумов функций
Часто бывает необходимо найти минимум или максимум заданной функции. Для поиска минимума или максимума функции как одной, так и нескольких переменных можно использовать стандартные средства Maple – minimize и maximize.
С помощью параметров можно задавать дополнительные данные для поиска, так, например, ограничить область поиска или, используя параметр location, включить расширенный вывод результатов – выводить не только значение минимума (или максимума), но и значения переменных в этой точке.
Рассмотрим поиск максимума функции на примере функции двух переменных.
| > | restart:
f:=(x,y)->-x^2+3*x-y^2-3*y-3; Fmax:=maximize(f(x,y)); maximize(f(x,y), location); X:=rhs(op(1,op(1,(op(1,%[2]))))); Y:=rhs(op(2,op(1,(op(1,%%[2]))))); |
 |
 |
![`/`(3, 2), {[{x = `/`(3, 2), y = -`/`(3, 2)}, `/`(3, 2)]}](images/Maple_528.gif){kind=small} |
 |
 |
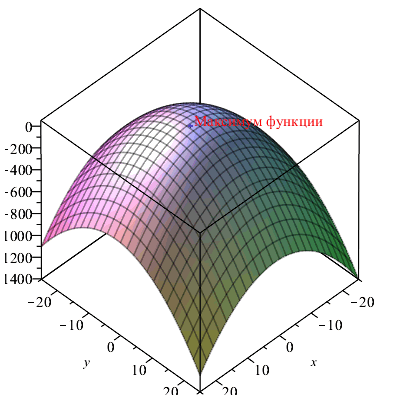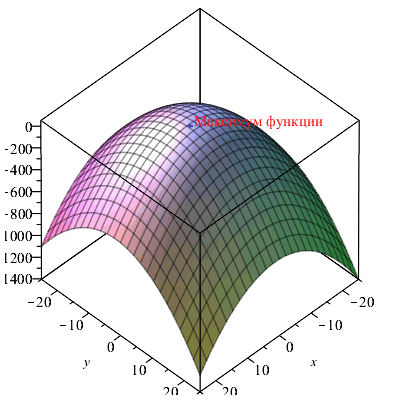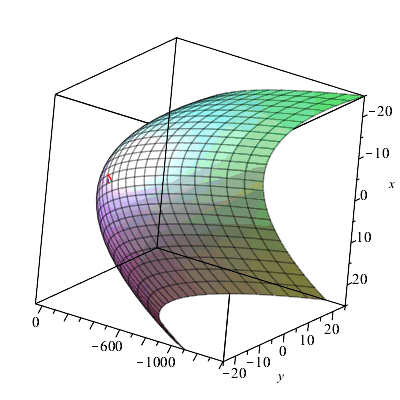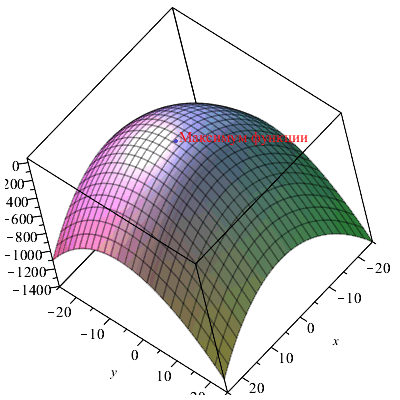
Приведем иллюстрацию последнего примера. Для этого построим функцию f (x, y), отобразим найденную точку максимума и снабдим поясняющей надписью.
| > | Fun:=plot3d(f(x,y),x=-25..25,y=-25..25,axes=boxed):
P_max:=plottools[sphere]([X,Y,Fmax],1,color=blue): txt:=plots[textplot3d]([X,Y,Fmax,"Максимум функции"],align = right,color=red): plots[display](Fun,P_max,txt); |
 |
Функция extrema позволяет найти экстремумы (как максимумы, так и минимумы) выражения при ограничениях или без них. При отсутствии ограничений вместо них записывается пустое множество {}. Найденные координаты точек экстремума присваиваются переменной `s`. Далее приведем пример применения функции extrema.
| > | restart:
z:=(x,y)->x^3+4*x*y^2-12*x-12*y+2; minimize(z(x,y)); maximize(z(x,y)); extrema(z(x,y),{},{x,y},`s`); s; |
 |
 |
 |
 |
 |
Приведем иллюстрацию последнего примера.
| > | Z:=plot3d(z(x,y),x=-5..5,y=-5..5,axes=boxed):
P1:=plottools[sphere]([-1,-3/2,z(-1,-3/2)],0.25, color=red): P2:=plottools[sphere]([1,3/2,z(1,3/2)],0.25, color=red): P3:=plottools[sphere]([sqrt(3),sqrt(3)/2,z(sqrt(3),sqrt(3)/2)],0.25, color=red): P4:=plottools[sphere]([-sqrt(3),-sqrt(3)/2,z(-sqrt(3),-sqrt(3)/2)],0.25, color=red): plots[display]({Z,P1,P2,P3,P4},title="Экстремумы функции"); |
 |
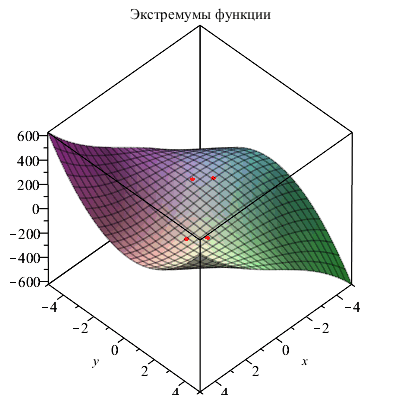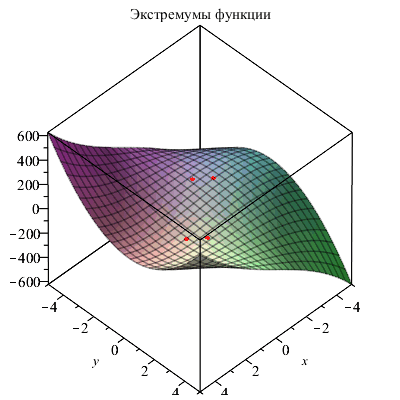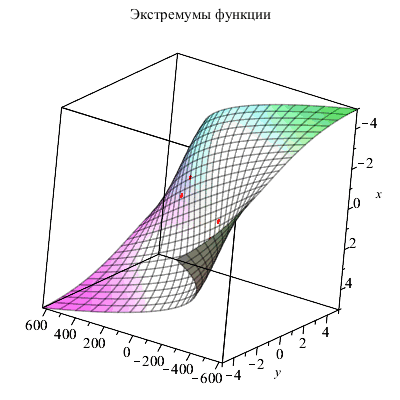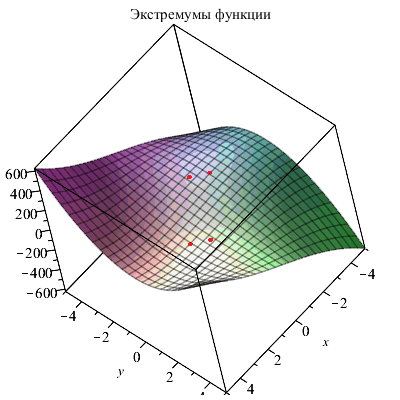Функции minimize и maximize определили минимум и максимум функции как -∞ и ∞, в то время как функция extrema нашла локальные экстремумы.