Численное решение дифференциальных уравнений в частных производных 

Для численного решения дифференциальных уравнений в частных производных используется функция pdsolve с параметром numeric. Рассмотрим следующую задачу. 

Струна длиной l кругового поперечного сечения радиусом с жестко закрепленными концами в начальный момент времени имела форму квадратичной параболы, симметричной относительно перпендикуляра к середине струны, а затем отпущена без толчка. Натяжение струны H. Длина струны l = 0,78 м. Плотность материала струны ρ = 6200 кг/. Определить процесс поперечных колебаний струны, если максимальное начальное отклонение струны составляло . 

Граничные условия определяют условия закрепления струны. В нашем случае струна закреплена на концах, т.е. и . 

Начальные условия определяют форму и скорость струны в начальный момент времени. В нашем случае – квадратичная парабола, определение коэффициентов которой является тривиальной задачей, а с учетом того, что струна отпущена без толчка – скорость всех ее точек в начальный момент времени равна нулю, т.е. и  

Граничные условия вместе с начальными условиями называют краевыми условиями. 

Поперечные колебания струны описываются волновым уравнением. 

>	restart: PDE:=diff(u(x,t),t,t)=a^2*diff(u(x,t),x,x);

 

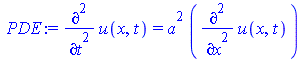>	a:=sqrt(T/rho[l]); rho[l]:=rho[c]*S; S:=Pi*r^2;

 

Введем исходные данные. 

>	T:=50;L:=0.78;r:=L/400;rho[c]:=6200;h:=L/100;

 

Форма струны в начальный момент времени. 

>	f:=-4*h/L^2*x^2+4*h/L*x;

 

Запишем краевые условия. 

>	BC:={u(0,t)=0,u(L,t)=0,u(x,0)=f,D[2](u)(x,0)=0};

 

Получим решение в виде модуля, который может быть использован для вывода численного решения в различных вариантах. 

>	SOL:=pdsolve(PDE,BC,numeric,timestep=1/2000, spacestep=1/2000);

 

Параметры timestep и spacestep задают шаги по времени и пространству, используемые при интегрировании уравнений в частных производных. 

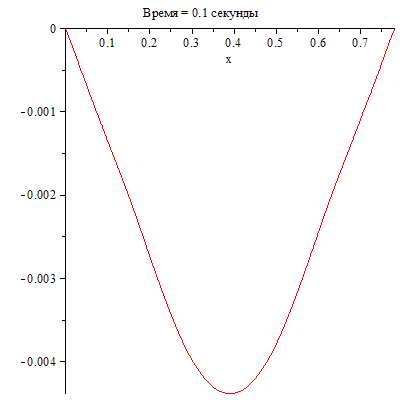
Покажем положение струны в момент времени t = 0,1 с , используя полученный модуль с параметром plot. 

>	SOL:-plot(t=0.1,title="Время = 0.1 секунды");

 

Визуализируем процесс колебаний струны, используя полученный модуль с параметром animate. 

>	SOL:-animate(t=0..0.5,frames=300,title="Время = %f");

 

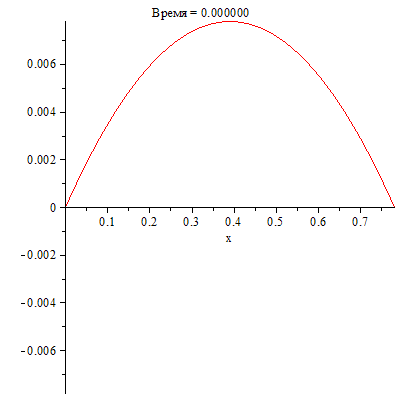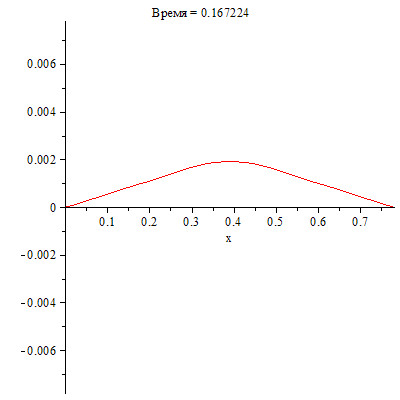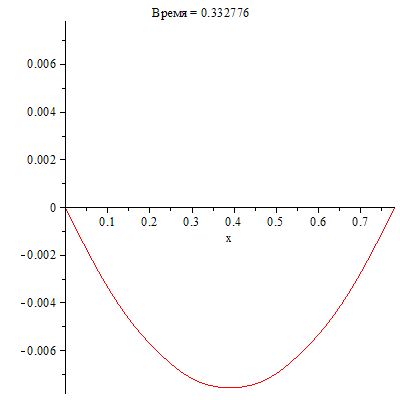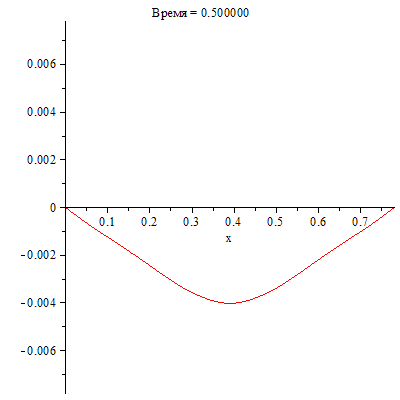Задача о поперечных колебаниях струны может быть решена методом Фурье. 

Метод Фурье является классическим методом решения уравнений в частных производных. Применительно к  рассматриваемой задаче решение представляется в виде 

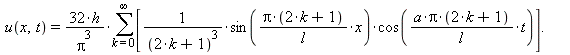
Ограничимся первыми двумястами членами бесконечной суммы и запишем решение.  

>	u:=(x,t)->32*h*(sum((sin(Pi*(2*k+1)*x/L)*cos(a*Pi*(2*k+1)*t/L)/(2*k+1)^3), k = 0..200))/Pi^3;

 

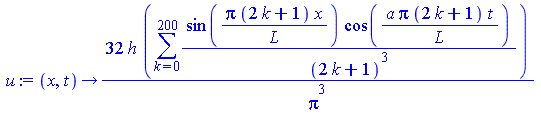Визуализируем процесс колебаний струны. 

>	plots[animate](plot,[(evalf(u(x,t)),x=0..L)],t=0..0.5,frames=300);

 

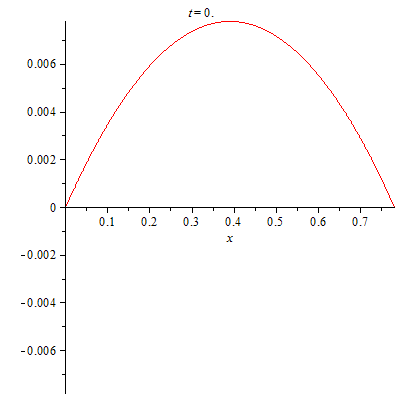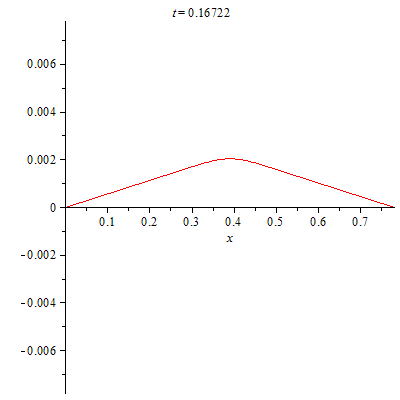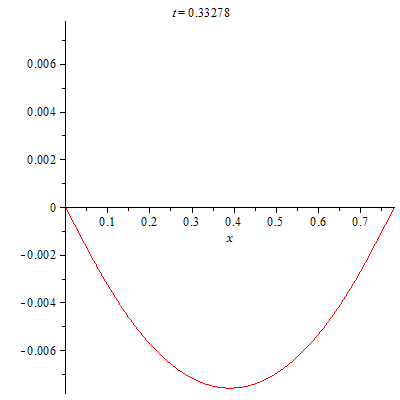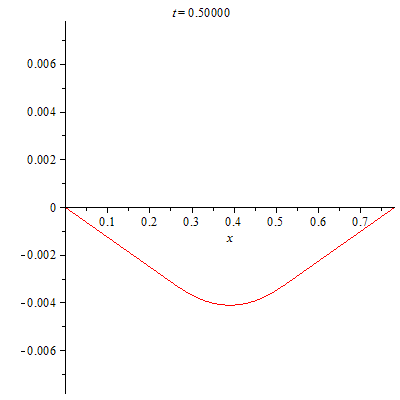Совместим два решения задачи. 

>	SOL_n:=SOL:-animate(t=0.5,frames=300,title="Время = %f",legend=["численный метод"]): SOL_a:=plots[animate](evalf(u(x,t)),x=0..L,t=0..0.5,frames=300,color=blue,legend=["метод Фурье"]): plots[display](SOL_a, SOL_n);

 

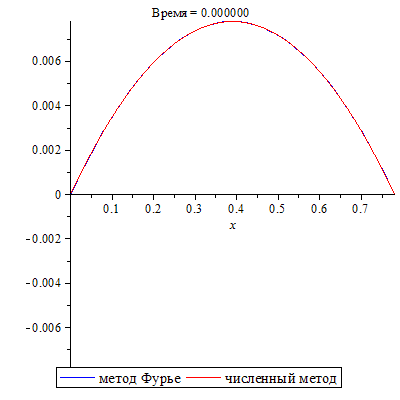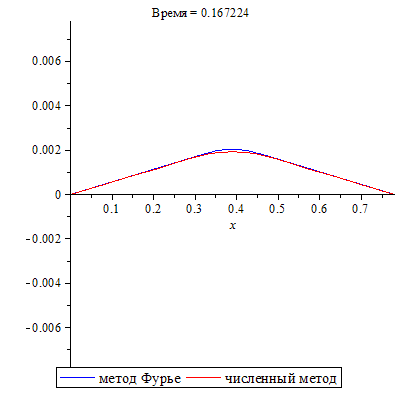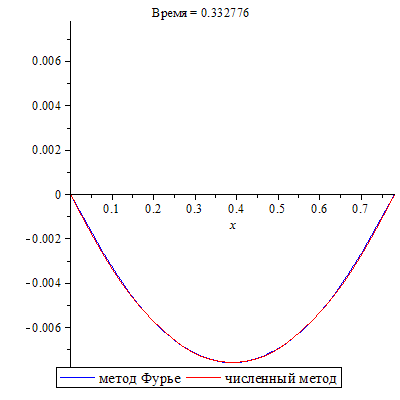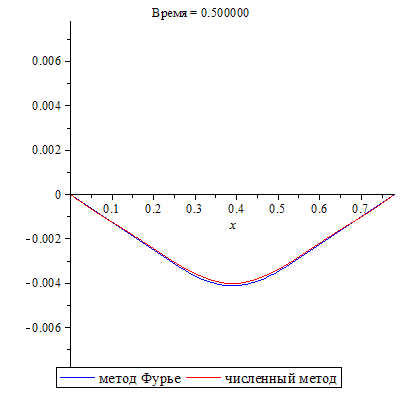Наблюдается отличное совпадение результатов, полученных разными методами.