Решение дифференциальных уравнений в частных производных 

Для решения дифференциальных уравнений в частных производных используется функция pdsolve (PDE, [u (x, y)], [параметры]), где PDE – дифференциальное уравнение в частных производных, u (x, y) – искомая функция нескольких переменных. 

Параметры выполняют приблизительно ту же роль, что и в функции dsolve, и более подробно о них будет рассказано ниже. 

Для решения системы дифференциальных уравнений в частных производных в качестве первых двух параметров следует использовать множества или списки с уравнениями и искомыми функциями. 

Типичной особенностью дифференциальных уравнений в частных производных и их систем является то, что для однозначного определения частного решения здесь требуется задание не значений того или иного конечного числа параметров, а некоторых функций. Найдем общее решением уравнения . 

>	restart: PDE:=diff(u(x,t),t,t)= diff(u(x,t),x,x); pdsolve(PDE,u(x,t));

 

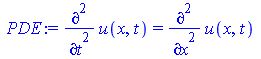Таким образом, рассмотренное дифференциальное уравнение лишь в той мере ограничивает произвол в выборе функций двух переменных u, что ее удается выразить через сумму двух функций _F1 и _F2 от одного переменного, которые остаются произвольными, если не дано каких-либо дополнительных условий. 

Если требуется найти решение в виде произведения функций, то следует использовать параметр HINT = `*`. 

>	pdsolve(PDE,u(x,t),HINT=`*`);

 

При использовании параметра build – Maple попытается записать решение в явном виде. 

>	pdsolve(PDE,u(x,t),HINT=`*`, build);

 

Здесь _C1, _C2, _C3, _C4 и _c1 – постоянные интегрирования, которые определяются из так называемых краевых или начальных условий, позволяющих однозначно выделить интересующее решение. В то время как краевые условия задаются исключительно на граничных точках области, где ищется решение, начальные условия могут оказаться заданными на определенном множестве точек внутри области. 

Пусть требуется найти функцию F (x, y), удовлетворяющую уравнению Лапласа  , если известно, что на окружности значения функции могут быть рассчитаны по выражению . 

Учитывая, что граничные условия заданы на окружности, целесообразно решать задачу в полярных координатах. Для преобразования дифференциального уравнения в полярную систему координат используем функцию PDEchangecoords из пакета Detools, а для преобразования граничных условий – функцию dchange из пакета PDEtools. 

>	restart: PDE:=diff(F(x,y),x,x)+diff(F(x,y),y,y); PDE:=DEtools[PDEchangecoords](PDE,[x,y],polar, [r,phi]); dp:={x=r*cos(phi),y=r*sin(phi)}; f:=x^2*y^2; f:=PDEtools[dchange](dp,f);

 

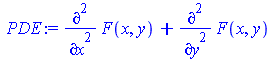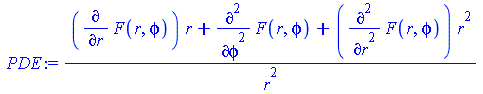Получаем решение в явном виде. 

>	R:=rhs(pdsolve(PDE,HINT=`*`,build));

 

Будем считать, что искомая функция определена во всех точках действительной плоскости, включая центр координат, т.е. при r = 0. Следовательно, _C2=0, т.к. в противном случае знаменатель в двух последних слагаемых решения обращается в ноль. 

>	_C2:=0; R;

 

Первое и второе слагаемое содержат произведение двух констант, поэтому можно считать, что _C1 = 1 и искать только _C3 и _C4. 

>	_C1:=1; R;

 

Для нахождения констант _C3 и _C4 используем граничные условия. 

>	simplify(subs({phi=0,r=4},R))=eval(subs({phi=0,r=4},f)); simplify(subs({phi=Pi,r=4},R))=eval(subs({phi=Pi,r=4},f)); solve({%,%%},{_C3,_C4});

 

Очевидно, что найденное решение не удовлетворяет граничным условиям. Также отметим, функция pdsolve находит решение с точностью до некоторой постоянной. Поэтому добавим к полученному ранее решению постоянную Z, подлежащую определению. 

>

R:=R+Z;

 

Для нахождения констант _C3, _C4 и Z используем граничные условия. Составим три уравнения и решим их совместно. 

>	R1:=subs(r=4,R=f); U1:=simplify(subs(phi=0,R1)); U2:=simplify(subs(phi=Pi/2/_c[1]^(1/2),R1)); U3:=simplify(subs(phi=Pi/4,R1)); S:=solve({U1,U2,U3},{_C3,_C4,Z});

 

Подставим найденные константы в решение. 

>	R1:=simplify(subs(S,R1));

 

Используя еще раз граничное условие , найдем константу . 

>	R2:=eval(subs(phi=Pi,R1)); solve(R2,_c[1]);

 

 

Warning, solutions may have been lost

 

Функция solve выдала предупреждение о возможной потере решений и не нашла ни одного решения уравнения!  

Для упрощения уравнения введем замену  , наложив дополнительное ограничение − C > 0 с помощью функции assume . 

>	assume(C>0): R2:=simplify(subs(_c[1]=C^2,%));

 

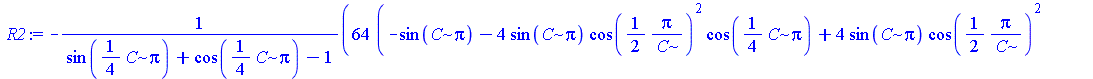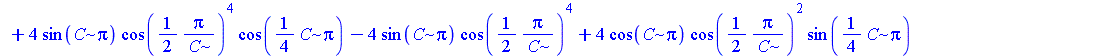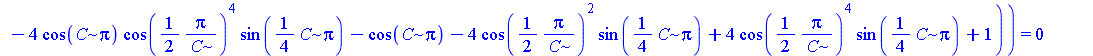Тильда после имени  переменной (C~) означает, что на переменную наложены ограничения. 

Попробуем еще раз решить уравнение с помощью функции solve, но уже относительно переменной C. 

>	solve(R2,C);

 

 

Warning, solve may be ignoring assumptions on the input variables.

Warning, solutions may have been lost

 

Результат тот же − решение не найдено! 

Для решения этого уравнения воспользуемся  более мощным средством −  Engine из пакета SolveTools и преобразуем полученное решение к виду с плавающей точкой. 

>	SolveTools:-Engine({R2},{C}); evalf(%);

 

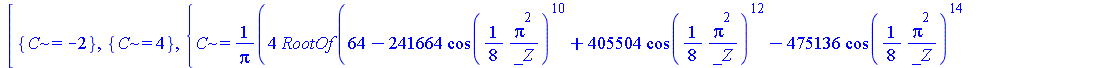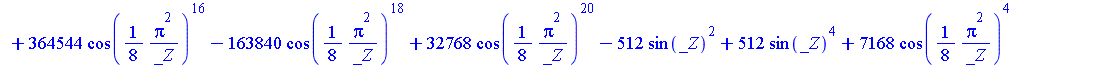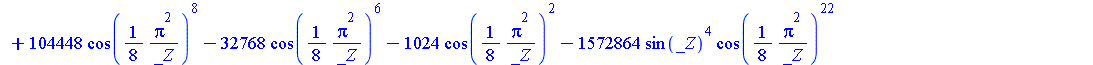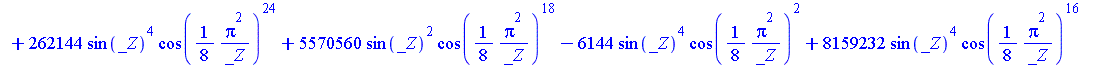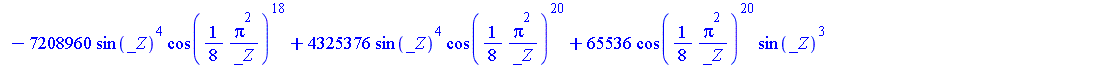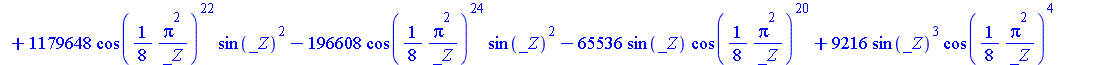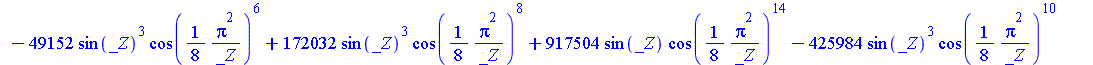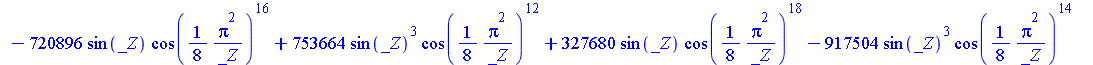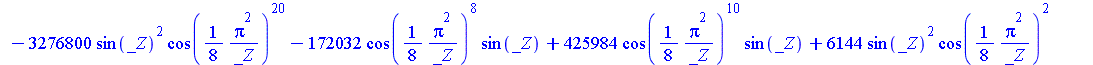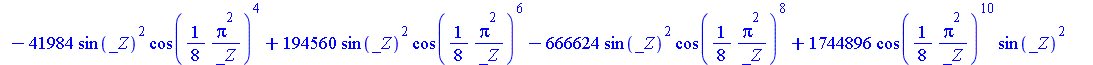С учетом ранее сделанной замены  получим значения  

Подстановка констант _C3, _C4, Z (все три константы хранятся в переменной S)  и  в общее решение  приводит к неопределенности типа . 

>	simplify(subs(S,R)): simplify(subs({_c[1]=4},%));

 

Error, (in simplify/recurse) indeterminate expression of the form 0/0

 

Подстановка констант _C3, _C4, Z  и  в общее решение приводит к решению задачи. Для упрощения полученного выражения применим функцию combine – мощное средство преобразования тригонометрических и ряда других выражений. 

>	simplify(subs(S,R)); simplify(subs({_c[1]=16},%)); SOL_p:=combine(%);

 

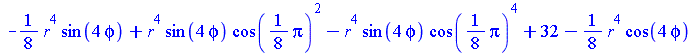Получено решение задачи в полярной системе координат. Нетрудно убедиться, что найденное решение удовлетворяет как уравнению Лапласа, так и граничным условиям. Преобразуем решение в декартову систему координат, используя известную связь между полярной и декартовой системами. 

>	pd:={r=sqrt(x^2+y^2),phi=arctan(y/x)}; SOL_d:=PDEtools[dchange](pd,SOL_p);

 

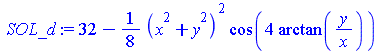Воспользуемся тригонометрическим тождеством 

>	cos(4*arctan(y/x))=op(3,trigsubs(cos(4*arctan(y/x)))); subs(%,SOL_d);

 

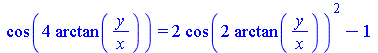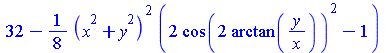Воспользуемся еще одним тригонометрическим тождеством, и после упрощения выражения получим окончательное решение. 

>	cos(2*arctan(y/x))^2 = op(11,trigsubs(cos(2*arctan(y/x))^2)); SOL:=simplify(subs(%,%%));

 

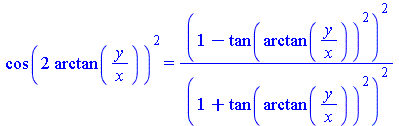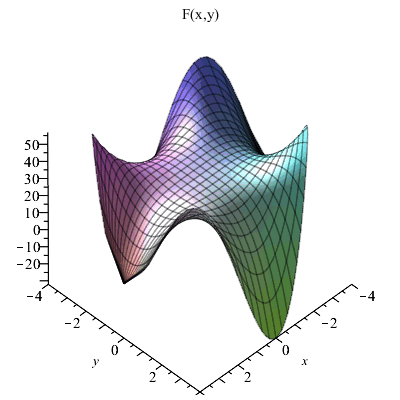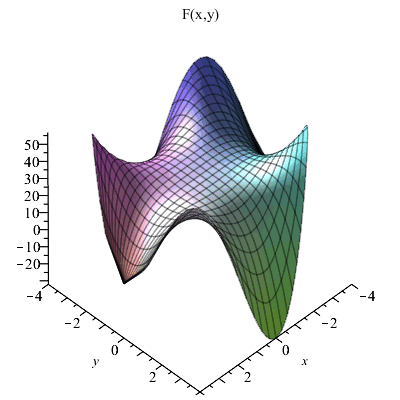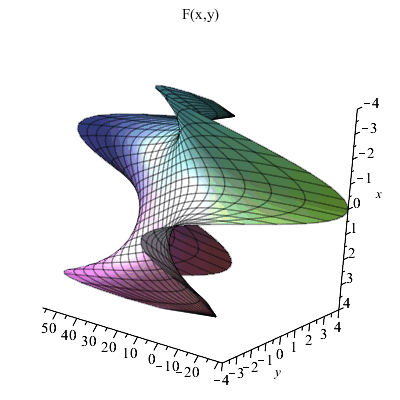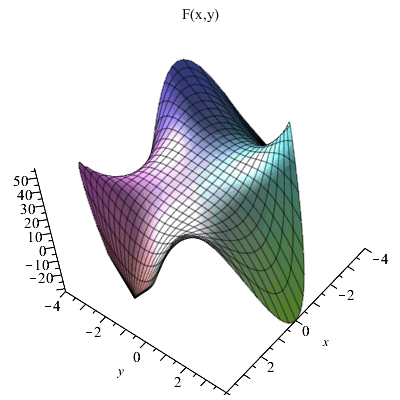
Окончательно запишем решение как функцию F ( x, y). 

>	F:=unapply(SOL,x,y);

 

Построим полученное решение в круге радиусом 4. 

>	plot3d(F(x,y),x=-4..4,y=-sqrt(16-x^2)..sqrt(16-x^2),axes=framed,title="F(x,y)");

 

Как показывает рассмотренный пример, даже имея в распоряжении такое мощное средство как Maple, задача получается достаточно трудоемкой, требующей определенного уровня математических знаний и опыта.