Решение обыкновенных дифференциальных уравнений 

Для решения обыкновенных дифференциальных уравнений используется функция  dsolve(ODE, [y (x)], [параметры]), где ODE – обыкновенное дифференциальное уравнение, y (x) – искомая функция. 

Параметры задаются в форме ключевое слово = значение. Ключевое слово может быть опущено, и в этом случае параметром будет являться только значение. 

Функция dsolve позволяет найти решение многих дифференциальных уравнений. По умолчанию dsolve пытается найти точное (аналитическое) решение. Однако, если точное решение не может быть получено, то можно попытаться найти приближенное решение с помощью разложения в ряд (параметр type = series) или численным методом (параметр type = numeric). 

Найдем общее решение дифференциального уравнения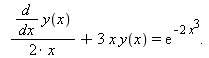  

>	restart: ODE:=diff(y(x),x)/(2*x)+3*x*y(x)=exp(-2*x^3); dsolve(ODE);

 

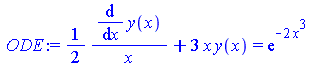Найдено общее решение дифференциального уравнения. Отметим, что исходное дифференциальное уравнение содержало только одну функцию – y ( x), относительно которой возможно решение, поэтому в функции dsolve второй параметр может быть опущен. 

Найдем частное решение дифференциального уравнения при условии, что y (0) = 5. Можно определить постоянную интегрирования (Maple обозначил ее _C1), используя уже полученное решение дифференциального уравнения и дополнительное условие. Но если в качестве первого параметра в функции dsolve подставить множество или список из дифференциального уравнения и дополнительного условия, то Maple сразу найдет частное решение дифференциального уравнения. 

>	R1:=dsolve({ODE,y(0)=5});

 

Найдем решение рассмотренного выше дифференциального уравнения с помощью рядов. Предварительно установим максимальную степень ряда – 16, напомним, что по умолчанию это значение равно 6. 

>	Order:=16: R2:=dsolve({ODE,y(0)=5},y(x),series);

 

Используя полученное в виде ряда решение, организуем список из координат точек в диапазоне x от 0 до 1 для последующего вывода этих точек функцией plot. 

>	R2p:=[seq([i/25,subs(x=i/25,op(2,convert(R2,polynom)))],i=0..25)]:

 

Найдем решение дифференциального уравнения численным методом. Maple умеет решать дифференциальные уравнения различными численными методами. По умолчанию используется метод Рунге – Кутта четвертого - пятого порядка. 

>	R3:=dsolve({ODE,y(0)=5},numeric);

 

При численном решении дифференциальных уравнений функция dsolve создает процедуру. При вызове процедуры, при подстановке в качестве параметра значения аргумента, выводится список, состоящий из аргумента и соответствующего значения функции. В общем случае, при численном решении дифференциальных уравнений n-го порядка, также выводятся значения всех производных до (n -1)-го порядка. 

>

R3(0.12);

 

Используя полученное в виде процедуры решение, организуем список из координат точек в диапазоне x от 0 до 1 для последующего вывода этих точек  функцией plot. 

>	R3p:=[seq([i/25+0.02,op(2,op(2,R3(i/25+0.02)))],i=0..25)]:

 

Совместим на одной координатной плоскости аналитическое решение, решение c помощью ряда и численное решение. 

>	plot([rhs(R1),R2p,R3p], x=0..1, style=[line,point,point], color=[red,blue,black],symbol=[box, circle], symbolsize=[15,15],legend=["аналитичесое решение", "разложение в ряд","численное решение"]);

 

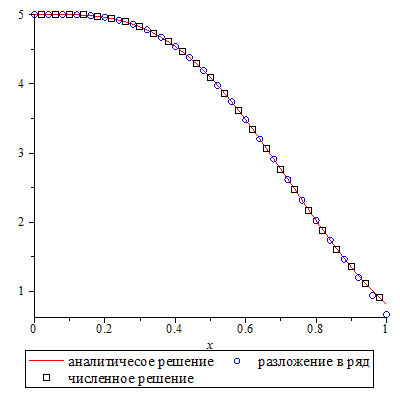Обратим внимание на следующие параметры функции plot: 

• symbol – способ отображения точек;

• symbolsize – размер точек (по умолчанию − 10);

• legend – подрисуночная надпись (легенда).

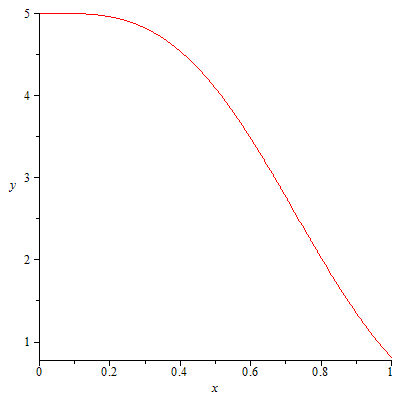
Для визуализации численных решений дифференциальных уравнений в пакете plots имеется функция odeplot. В предыдущем примере для построения решения на интервале от 0 до 1 функцию odeplot можно использовать следующим образом: 

>	plots[odeplot](R3,0..1);

 

Рассмотрим задачу, для решения которой требуется составить и решить дифференциальное уравнение. 

Установлено, что скорость распада радия прямо пропорциональна его количеству в каждый момент времени. Определить закон изменения массы радия в зависимости от времени, если при t = 0 масса радия была . 

Скорость распада в момент времени t по условию задачи определяется выражением где k – коэффициент пропорциональности (k > 0). Знак «минус» ставится потому, что при увеличении времени масса радия убывает,  

Отметим, что масса радия – функция времени m (t)  и по условию задачи m (0) =. 

>	restart: diff(m(t),t)=-k*m(t); dsolve({%,m(0)=m[0]});

 

Также было экспериментально определено, что для радия k = 0,000436 (единица измерения времени − год). Подставим в последнее выражение 

>	subs(k=0.000436,%);

 

Найдем период полураспада радия, т.е. промежуток времени, за который распадается половина первоначальной массы. Подставим в последнюю формулу вместо m значение , а вместо t – T, получим 

>	subs({m(t)=m[0]/2,t=T},%);

 

Решим последнее уравнение относительно T, получим период полураспада радия (в годах ). 

>	solve(%,T);