Пакет для обучения математике 

В Maple имеется пакет student, предназначенный для обучения математике. Он содержит набор функций, предназначенных для выполнения расчетов шаг за шагом, так, чтобы была понятна последовательность действий, приводящих к результату. 

Функция intparts – интегрирование по частям. 

>	restart: with(student): Int(x*cos(x),x); intparts(Int(x*cos(x),x),x); value(%);

 

Интегрирование подстановкой – функция changevar. 

>	Int((cos(x)+1)^3*sin(x), x); ch:=cos(x)+1; changevar(ch=u, Int((cos(x)+1)^3*sin(x), x), u); value(%); subs(u=ch,%);

 

В примере использована подстановка  cos ( x) + 1 = u. 

Функция subs, синтаксис которой следующий − subs( старое_выражение = новое_выражение, выражение ), использована для возвращения к исходной переменной x. 

>	Int(sqrt(1-x^2), x=a...b); changevar(x=sin(u), Int(sqrt(1-x^2), x=a...b), u); value(%);

 

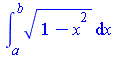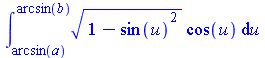Использована подстановка x = sin ( u). Заметим, что  пределы интегрирования изменились автоматически. 

Для вычисления двойных и тройных интегралов служат функции Doubleint и Tripleint. 

>	Tripleint((r^2*sin(f),r=0..4*cos(f),f=0..Pi/4,t=0..Pi/2)): %=value(%);

 

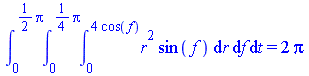Функции simpson и trapezoid реализуют числовое приближение к интегралу методами Симпсона и трапеций (n − число интервалов). 

>	simpson(x^k*ln(x), x=a..b, n);

 

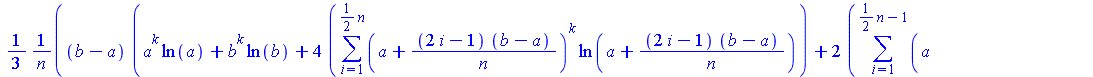>	trapezoid(x^k*ln(x), x=a..b, n);

 

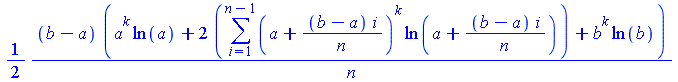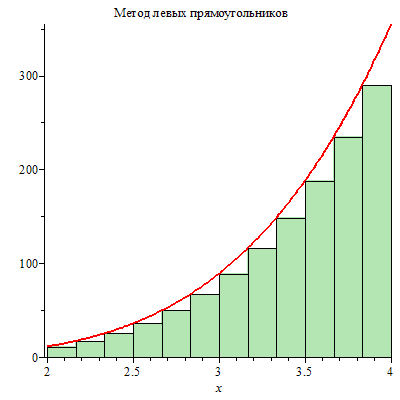
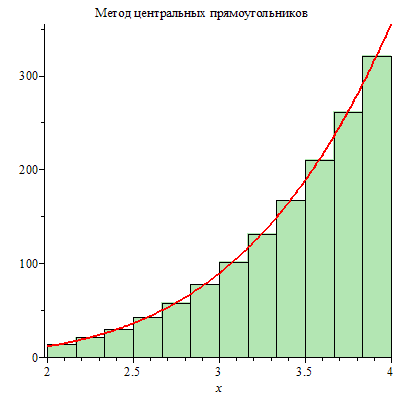
Функции leftbox, middlebox и rightbox иллюстрируют интегрирование методами левых, центральных и правых прямоугольников. Необязательный параметр title позволяет задать заголовок рисунка. 

>	leftbox(x^4*ln(x), x=2..4, 12, title="Метод левых прямоугольников"); middlebox(x^4*ln(x), x=2..4, 12, title="Метод центральных прямоугольников"); rightbox(x^4*ln(x), x=2..4, 12,title="Метод правых прямоугольников");

 

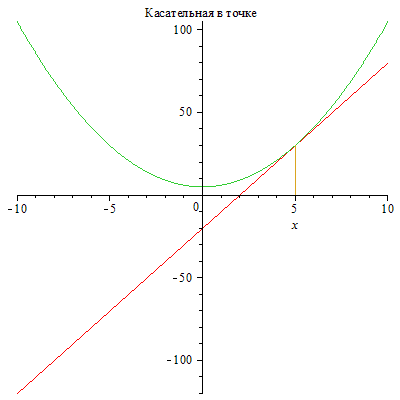
Функция showtangent строит график функции и касательную в указанной точке. 

>	showtangent(x^2+5, x = 5,title="Касательная в точке");